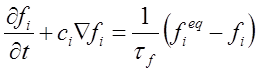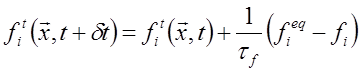What is the Lattice Boltzmann method (LBM)?

Lattice Boltzmann method is a class of computational fluid dynamics (CFD) methods for fluid flow simulation. Instead of solving the Navier-Stokes equations, LBM solves the discrete Boltzmann equation to simulate the flow of a Newtonian fluid with collision models such as Bhatnagar-Gross-Krook (BGK).

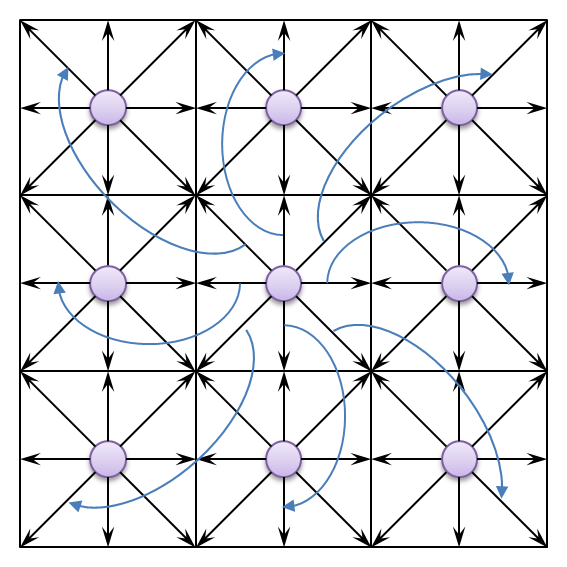
A D2Q9 lattice Boltzmann model on a lattice showing collision and streaming process.

Algorithm with BGKW approximation

It is nearly impossible to solve the Boltzmann equation because its collision term is extremely complicated. However, the outcome of two-body collisions is not likely to significantly influence the values of many measured quantities (Cercignani, 1990). Hence, it is possible to approximate the collision term with a simple operator without introducing significant error to the solution. Bhatnagar, Gross, and Krook (BGK) in 1954 introduced a simplified model for collision operator. At the same time Welander (1954), independently, introduced similiar operator. The collision operator is replaced as:

By introducing BGKW approximation, the Boltzmann equation (without external forces) can be approximated as:

In the computer algorithm, the collision and streaming step are defined as follows:

collision :

streaming :

Two-dimensional characteristic boundary conditions for open boundaries in the lattice Boltzmann methods

In the LBM, most recent researches on the boundary conditions have focused on developing high-order boundary schemes for various configurations, while little attention was paid on the treatment of spurious reflections at the open. The two-dimensional (2-D) characteristic boundary conditions (CBC)  based on the characteristic analysis are formulated for the lattice Boltzmann methods LBM. In this approach, the classical locally-one dimensional inviscid (LODI) relations are improved by recovering multi-dimensional effects on flows at open boundaries. The 2-D CBC are extended to a general subsonic flow configuration in the LBM and the effects of the transverse terms are clarified.

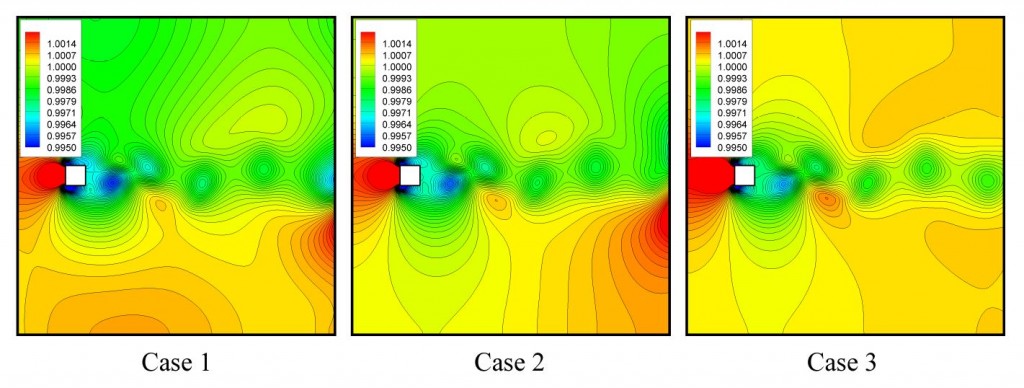
Vortex-shedding over a square block with different characteristic boundary conditions (CBC), which was simulated with 2-D isothermal multi-relaxation time lattice Boltzmann method (MRT-LBM): Case 1-Conventional CBC (Poinsot and Lele), Case 2-Thompson’s CBC, and Case 3-Improved CBC.